Jump Crypto recently released a blog post on Shelby, a decentralized storage system designed to store and serve data reliably and efficiently. This post shares why we believe this is possible at prices that are competitive with existing Web2 providers, like AWS and GCP. This post is NOT intended to indicate actual prices, or even price model (both of which may vary wildly from anything discussed in this post); it merely shows that profitability is possible at prices competitive with existing Web2 solutions, given projected infrastructure costs.

Required Components

Before jumping into costs and benefits, we first need to understand what the different components of Shelby are. To build a competitive storage system, Shelby requires 3 core components: the Aptos blockchain, remote procedure call/access nodes (RPCs), and storage provider nodes (SPs). The Aptos blockchain provides the byzantine fault-tolerance and decentralized ledger required to make this a viable business, the RPCs provide an interface through which users can interact with Shelby, and SPs perform the actual storage of the data. For more details on the architecture, please see the whitepaper.

Expected Benefits

In decentralized systems, individual organizations run major infrastructure components. Protocol designers must make the incentives to do so attractive to encourage participation. Now, we look at the benefits each component can expect to receive. We do not compute exact numbers in this section, instead computing symbolically and leaving exact numbers to a later section.

Aptos Blockchain

Every time a user wishes to write a new blob onto Shelby, they must interact with the Aptos blockchain and pay a nominal gas fee to do so. While the fee is small for individual transactions, we anticipate that the volume of interactions means this fee is significant enough to ensure that the total of all fees collected is enough to be considered. We do not include the blockchain earnings as part of the modeling.

For metadata-heavy workloads, there may be significant interactions with the blockchain, which will therefore involve potentially heavy fees as well. We do not discuss this workflow here, instead focusing on the economics of reading and writing to Shelby.

RPCs

While each individual RPC is free to charge for payments in a method of its choosing, we anticipate that the vast majority of RPC income will come from read fees. Specifically, when a user pays Shelby some amount to read data, the RPC will keep some portion of these fees for itself and use the remaining fees to pay the SPs to retrieve the data. We call the portion of the fees that the RPC keeps \(F_{RPC}\), and the read fee per GB \(RF\). That is, per GB served, the RPC earns \(RF \cdot F_{RPC}\).

Next, we need to know how much data will be read from a given RPC. We assume that the number of RPCs in the system will grow to accommodate the total data that users wish to read. That is, due to network constraints, a given RPC is only capable of serving a set amount of data per month. We anticipate that the total number of RPCs can be found by simply dividing the total amount of data read from Shelby by the amount an individual RPC can serve. This implies the per RPC income is independent of the total volume of data read from the system. If we assume an average send rate of 1 Gbps over the course of a month, we get:

\begin{equation}DataSent_{RPC}=1 Gbps \cdot \frac{1 byte}{8 bits} \cdot 2592000 \frac{seconds}{month}\end{equation}

\begin{equation}DataSent_{RPC}=324000 \frac{GB}{month}\end{equation}

That is, we anticipate that each RPC will be serving 324,000 GB every month (note that we assume a 30-day month in the calculation of seconds per month above). Multiplying that by the earnings per GB for an RPC gives us the total earnings of the RPC per month, or:

\begin{equation}Earnings_{RPC}=324000\frac{GB}{month}\cdot RF\cdot F_{RPC}\end{equation}

SPs

Unlike RPCs, the income an SP receives will be directly correlated to the amount of data it holds. Specifically, an SP earns data both for storing the data and for serving to an RPC when asked. To ensure that data remains highly durable, we use erasure coding; this requires us to store \(R\) (for replication) bytes for every byte that a user wishes to store. Here, \(R\) is a parameter that is determined by choice of erasure coding scheme. Calling the write fee \(W\), the SP can therefore expect to be paid \(\frac{W}{R}\) for every byte that it stores.

An SP will also earn income for data that is read from it. The SP will earn \(\frac{RF}{R} \cdot (1 - F_{RPC}) \cdot TotalBytesRead\) in read revenues. If each byte stored is read on average \(RA\) (for read average) times, then \(TotalBytesRead=RA \cdot StoredBytes\). Combining the two, the total read revenues an SP will earn is \(\frac{RF}{R} \cdot (1 - F_{RPC}) \cdot RA \cdot StoredBytes\).

Combining earnings for both data that is stored and data that is read, we get the following for SP earnings:

\begin{equation}Earnings_{SP}=\frac{W}{R} \cdot StoredBytes + \frac{RF}{R} \cdot (1 - F_{RPC}) \cdot RA \cdot StoredBytes\end{equation}

\begin{equation}Earnings_{SP}=\frac{StoredBytes}{R} \cdot \bigg(W + RF \cdot (1 - F_{RPC}) \cdot RA \bigg) \end{equation}

Costs

RPCs

The easiest way to run an RPC would likely be to rent a dedicated server to run in a data center from providers such. Aside from this cost, there is also the cost of a private bandwidth provider (that will allow RPCs and SPs to communicate with each other with low latency and high bandwidth). Finally, there are costs associated with interacting with the Aptos blockchain, including the cost of running an Aptos full node, associated gas fees, etc. The total cost of the RPC is then just:

\begin{equation}Cost_{RPC}=ServerCost_{RPC}+Bandwidth_{RPC}+AptosCosts_{RPC}\end{equation}

If we assume that each RPC operator would like to earn \(Y_{RPC}\) of profit on their costs, the RPC operator will only be willing to participate if:

\begin{equation}Earnings_{RPC} \ge (1 + Y_{RPC}) \cdot Cost_{RPC}\end{equation}

\begin{equation}Earnings_{RPC} \ge (1 + Y_{RPC}) \cdot (ServerCost_{RPC}+Bandwidth_{RPC}+AptosCosts_{RPC})\end{equation}

This gives us a lower bound on how cheap we can make the read fees while remaining a profitable business from the perspective of an RPC operator.

SPs

Similarly, the easiest way to run an SP would also be to rent a dedicated server. SPs also incur a cost from the private bandwidth provider, and a cost associated with interacting with the Aptos blockchain. The total cost of the SP is then just:

\begin{equation}Cost_{SP}=ServerCost_{SP}+Bandwidth_{SP}+AptosCosts_{SP}\end{equation}

To ensure that SP incentives align with our intended goal (storage for data that is read frequently), we model the write fee such that SPs will only break even if no data is read; any profits SPs earn will be directly related to how often data is read. I.e., if no data is read from Shelby, an SP is modeled to only earn enough to exactly offset its operational cost listed above, or:

\begin{equation}EarningsWithoutReads_{SP}=Cost_{SP}\end{equation}

\begin{equation}EarningsWithoutReads_{SP}=ServerCost_{SP}+Bandwidth_{SP}+AptosCosts_{SP}\end{equation}

This gives us a write cost that ensures that SPs will never lose money, and ensures that SPs are incentivized to serve data quickly and promptly.

Reducing Number of Variables

Both the read fee inequality and the write fee inequality above have several variables; to reduce them, we make a few assumptions that we believe to be reasonable.

• \(Y_{RPC}=50\%=0.5\). We assume that RPC operators will want a 50% yield on their operational expenditures. E.g., if a given RPC operator spends $1000 a month to rent and run a server acting as an RPC node, they will want to earn at least $1500 a month in rewards to justify doing so
• \(R=2\). A higher replication factor allows the system to achieve higher durability levels, while a lower replication factor allows the system to be cheaper. In Web3 data availability solutions, replication factors tend to be 4.5 or even higher. Shelby does not aim to be yet another data availability layer, and instead aims to provide services more akin to AWS and GCP. Our Web2 competitors tend to use replication factors between 1.2 and 1.6. For our final product, we aim to have our replication factor more closely resemble that of our Web2 competitors, but for the sake of this blog post, we use a higher replication factor
• \(F_{RPC}=0.5\). We set the fraction of read rewards that RPC nodes get to be half of all read rewards. In principle, this is a business decision that individual RPCs and SPs need to negotiate between themselves; we simply make an easy assumption of “50-50” to start with
• \(Bandwidth_{RPC}=F_{PBP} \cdot Earnings_{RPC}\), \(Bandwidth_{SP}=F_{PBP} \cdot Earnings_{SP}\). That is, the private bandwidth provider charges a percentage of the earnings received by each node. We further assume, for the purpose of this document, that \(F_{PBP}=10\%=0.1\)
• \(AptosCosts_{RPC}=F_A \cdot Earnings_{RPC}\), \(AptosCosts_{SP}=F_A \cdot Earnings_{SP}\). A significant portion of the costs of interacting with the blockchain scale as the number of interactions grows. While there is some portion that does not, e.g., the cost of running an Aptos full node, here we model the entire cost as a fraction of the earnings (which is, in turn, correlated to the volume of interactions). Further, we assume that \(F_A=10\%=0.1\)

Plugging this back into our inequality for RPC earnings, we get:

\begin{equation}Earnings_{RPC} \ge (1 + Y_{RPC}) \cdot (ServerCost_{RPC} + Bandwidth_{RPC} + AptosCosts_{RPC})\end{equation}

\begin{align}Earnings_{RPC} \ge (1 + 0.5) \cdot (ServerCost_{RPC} &+ 0.1 \cdot Earnings_{RPC} \nonumber \\ &+ 0.1 \cdot Earnings_{RPC})\end{align}

\begin{equation}Earnings_{RPC} \ge 1.5 \cdot ServerCost_{RPC} + 0.3 \cdot Earnings_{RPC}\end{equation}

\begin{equation}0.7 \cdot Earnings_{RPC} \ge 1.5 \cdot ServerCost_{RPC}\end{equation}

\begin{equation}Earnings_{RPC} \ge \frac{15}{7} \cdot ServerCost_{RPC}\end{equation}

\begin{equation}324000 \cdot RF \cdot 0.5 \ge \frac{15}{7} \cdot ServerCost_{RPC}\end{equation}

\begin{equation}RF \ge \frac{1}{75600} \cdot ServerCost_{RPC}\end{equation}

Now, we look at SP costs and earnings with this set of assumptions as well.

\begin{equation}EarningsWithoutReads_{SP}=ServerCost_{SP}+Bandwidth_{SP}+AptosCosts_{SP}\end{equation}

\begin{align}EarningsWithoutReads_{SP}=ServerCost_{SP} &+0.1 \cdot Earnings_{SP} \nonumber \\ &+ 0.1 \cdot Earnings_{SP}\end{align}

\begin{equation}EarningsWithoutReads_{SP} - 0.2 \cdot Earnings_{SP} = ServerCost_{SP}\end{equation}

\begin{align}EarningsWithoutReads_{SP} - 0.2 \cdot (EarningsWithoutReads_{SP} &+ ReadEarnings_{SP}) \nonumber \\ &= ServerCost_{SP}\end{align}

\begin{equation}0.8 \cdot EarningsWithoutReads_{SP} - 0.2 \cdot ReadEarnings_{SP} = ServerCost_{SP}\end{equation}

Here, we make one more simplifying step. Specifically, we stated earlier that we wanted SPs to break even when there are no reads (and therefore all profits were modeled to be exactly the earnings from reads). As such, instead of relating the read earnings to the server cost, as in the equation above, we instead subtract it from the profits. That is, we have:

\begin{equation}0.8 \cdot EarningsWithoutReads_{SP} = ServerCost_{SP}\end{equation}

\begin{equation}Profit_{SP} =ReadEarnings_{SP}-0.2 \cdot ReadEarnings_{SP} = 0.8 \cdot ReadEarnings_{SP}\end{equation}

With that simplifying step, we can compute our write costs as:

\begin{equation}0.8 \cdot W \cdot \frac{StoredBytes}{2}=ServerCost_{SP}\end{equation}

\begin{equation}W=2.5\cdot \frac{ServerCost_{SP}}{StoredBytes}\end{equation}

Putting It All Together (with actual numbers!)

We look at several different scenarios and show how our prices would look in those scenarios.

Write Fee

We first start with the equation above that is a simple equality, the write fee. A minimal SP server needs to have enough capacity to store all the data, as well as some extra capacity (if another SP fails, we need to ensure that other SPs have enough capacity to store that extra data). We assume that, in the ideal case (no SP failures currently), an SP will only be at 80% capacity. Looking at, e.g., a server from OVHcloud, https://us.ovhcloud.com/bare-metal/advance/adv-stor/, or the screenshot below, we see that we can get a server that has 176 TB (8x22 TB) of raw capacity for $480 per month. A raw capacity of 176 TB indicates that we should only store a maximum of 140.8 TB on each server.

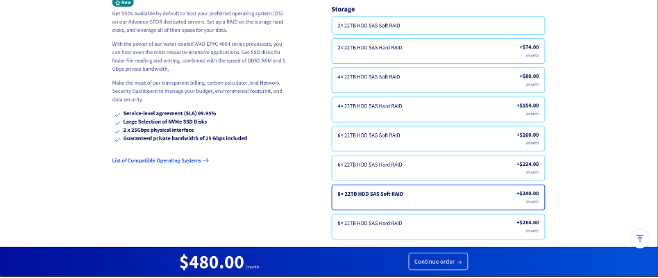
If we assume that each SP is asked to store 125 TB, or 125 * 1000 = 125000 GB, then we get:

\begin{equation}W=2.5 \cdot \frac{ServerCost_{SP}}{StoredBytes} \end{equation}

\begin{equation}W=2.5 \cdot \frac{480}{125000}=\frac{\$0.0096}{GB \cdot month}\end{equation}

We can also look at a more aggressive server/bytes stored combination. For example, the server found at https://us.ovhcloud.com/bare-metal/high-grade/hgr-stor-1/, or the screenshot below, for a price of $2079 per month can hold 792 TB of raw capacity (36 hard drives of 22 TB each). Given the considerations above, 792 TB of raw capacity means that each SP should hold a maximum of 633.6 TB of actual data.

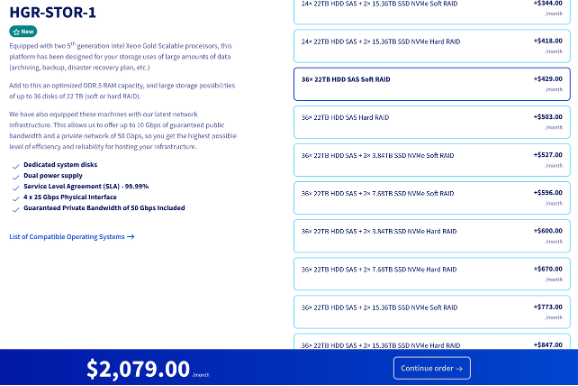
If we assume that each SP is asked to store 600 TB, or 600 * 1000 = 600000 GB, then we get:

\begin{equation}W=2.5 \cdot \frac{ServerCost_{SP}}{StoredBytes} \end{equation}

\begin{equation}W=2.5 \cdot \frac{2079}{600000} = \frac{\$0.0086625}{GB \cdot month}\end{equation}

We see that, as the amount stored on Shelby increases, the amount that we need to charge decreases. This is because \(StoredBytes\) is in the denominator; as it increases, the write fee naturally decreases. This is offset by the cost for the server in the numerator. If we plot this progression, we see the natural conclusion. (Note: There are occasional jumps UP in price in this chart. This is because the associated server cost went up. E.g., if we were only storing 30000 GB per SP, we can use a server that costs $240. Increase that to 40000 GB per SP, however, and that server becomes just too small. The server cost goes to $320 – that cost increase offsets the increase in data stored in the server.)

While the write fee will continue to decrease the more data we store, asymptotically approaching some minimum value, realistically, there is an upper bound in the total amount we can store per SP, meaning we are unlikely to ever approach the asymptote. Looking at the more realistic numbers we have above, then:

If nothing is read from Shelby, storage costs can be just under 1 cent per GB per month for SPs to break even on just write fees. The exact value depends primarily on how much storage is in use.

Introducing Reads

We are designing Shelby primarily for data that will be read frequently. In this section, then, we start looking at how the numbers change when we start introducing reads. To start, we look at the read fee (which does not depend on the total number of reads – we earlier assumed that each RPC node would get enough reads to always be able to send a set average bandwidth per month).

Read Fee

A minimal RPC server needs to have the capability to egress at least 324,000 GB of data a month and maintain some minimum level of compute to be able to encode and decode data as it is written or read, respectively. One such server, found at https://us.ovhcloud.com/bare-metal/scale/scale-a1/, or the screenshot below, costs $1041.

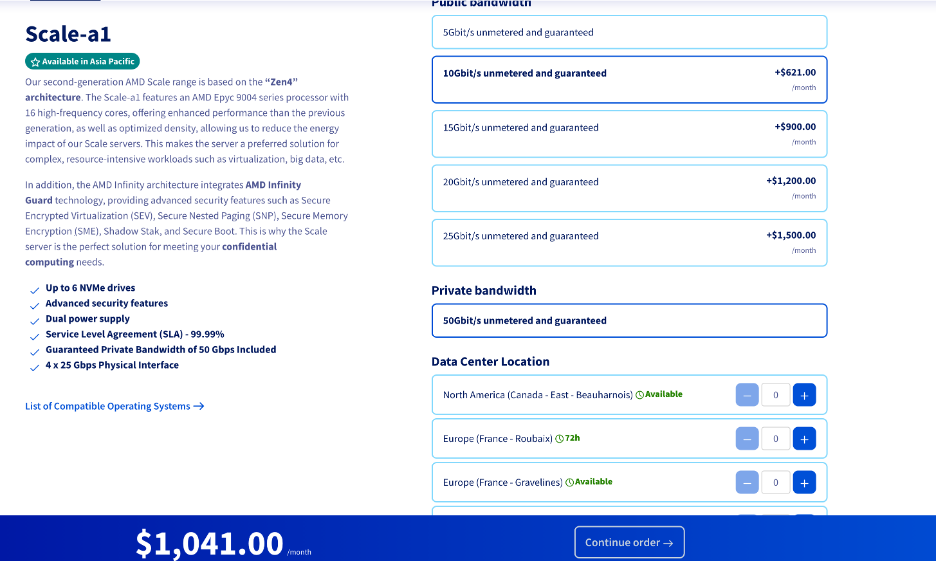
Plugging this into our read fee inequality, we get:

\begin{equation}RF \ge \frac{1}{75600} \cdot ServerCost_{RPC} \end{equation}

\begin{equation}RF \ge \frac{1041}{75600}\gtrapprox \frac{\$0.0138}{GB} \end{equation}

In other words, with our set of assumptions, RPC operators will be profitable for a read fee of just over 1 cent per GB.

SP Profits

In our model, the total SP profits is equal to exactly \(0.8 \cdot ReadEarnings_{SP}\). For example, using the minimum read fee computed above, and using the smaller of the two examples in the write fee section above, we have:

\begin{equation}Profits_{SP}=0.8 \cdot ReadEarnings_{SP} = 0.8 \cdot RF \cdot RA \cdot (1 - F_{RPC}) \cdot \frac{StoredBytes}{R}\end{equation}

\begin{equation}Profits_{SP} \approx 0.8 \cdot \frac{\$0.0138}{GB \cdot month} \cdot RA \cdot (1 - 0.5) \cdot \frac{125000}{2} \end{equation}

\begin{equation}Profits_{SP} \approx \$344.25 \cdot RA\end{equation}

If we estimate the average read rate of the data to be 4 (i.e., the average byte stored in Shelby is read 4 times per month), we get:

\begin{equation}Profits_{SP} \approx \$1377/month \end{equation}

Further, given public AWS S3 read pricing of $0.05 per GB egressed and $0.02 per GB per month for storage, the more an end-user wants to egress data, the more the end-user saves by switching to Shelby. This is illustrated in the graph below:

As the average read rate of data goes up, the total amount saved by swapping to Shelby (with its lower read fee) goes up. Similarly, the profits made by Shelby providers also goes up as the average read rate of data does. That is, the economic incentives for Shelby operators align with the economic incentives for Shelby users.

Conclusion

Shelby can be cost-competitive with our Web2 competitors. As shown above, with reasonable assumptions all our operators will be able to make a profit at prices that are below current market rates. Specifically, reads can be made profitable at a price of just over 1 cent per GB read. Writes can be made profitable at a price of just under 1 cent per GB per month.